
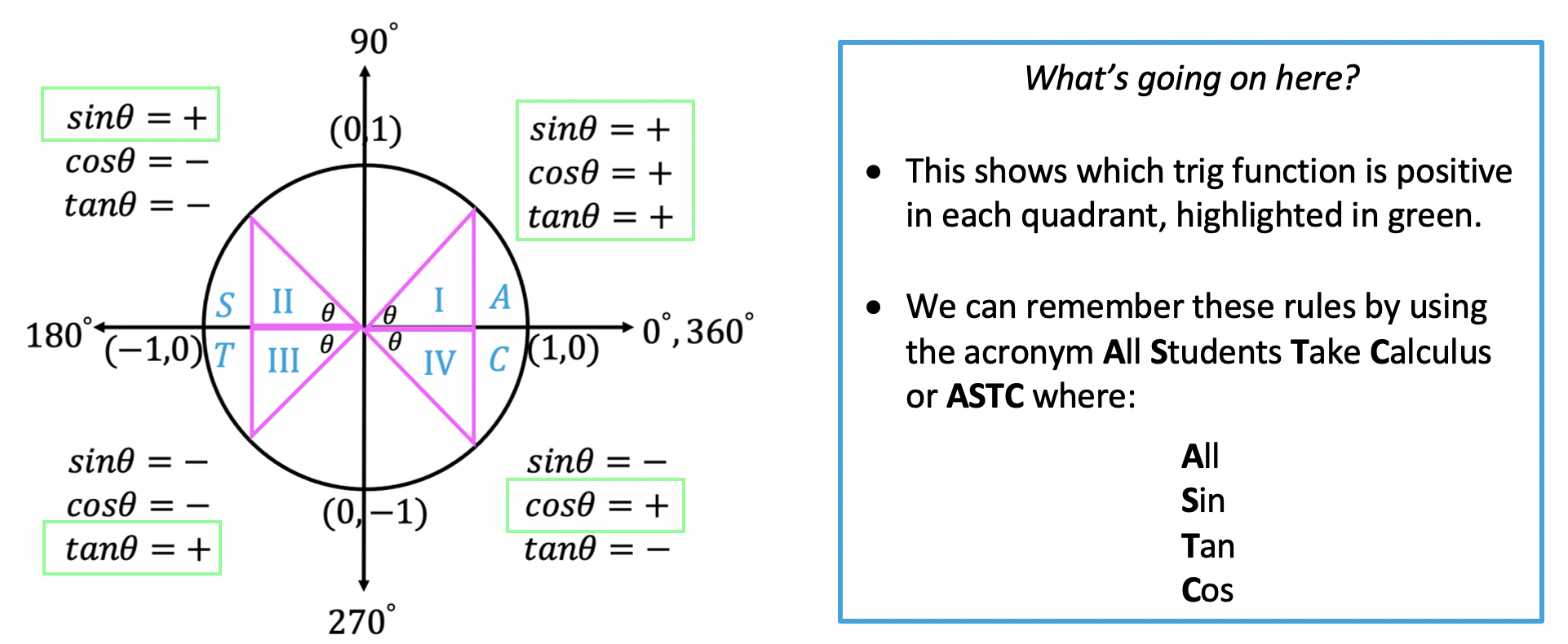
The code for the calculator contains some basic interactivity and error handling within constraints of the editor. It can be calculated with any desired accuracy. For quantitative relationships, since π radians = 180°, 1 radian would be 180°/ π or roughly 57°. They each have their advantages and disadvantages. You can choose degrees or radians as a measure of angle. It takes inputs for angle measures and outputs corresponding values for sine, cosine and tangent functions.

Trigonometric CalculatorĪs a useful practice tool, I have added a simple trigonometric calculator. Unit circle showing important sine and cosine values to rememberĪs a final note for this section, it always helps to remember the following trigonometric identity based on the Pythagorean theorem: sin 2(α) + cos 2(α) = 1. It reflects both positive and negative values for X and Y axes and shows important values you should remember Fig 7. Unit circle showing sin(45) = cos(45) = 1 / √2Īs a result of the numerator being the same as the denominator, tan(45) = 1.įinally, the general reference Unit Circle. Now the question you might ask: as sin goes from 0 to 1 while cosine goes from 1 to 0, do they ever equal each other? The answer is yes, and that happens exactly half way at 45 degrees! The circle looks like this: Fig 6. Therefore tan(90) is said to be undefined. What about tangent(90)? As the cosine measure approaches 0, and it happens to be a denominator in a fraction, the value of that fraction increases to infinity. Unit circle showing cos(90) = 0 and sin(90) = 1 The coordinates of the corresponding point are (0, 1). Next let's see what happens at 90 degrees. Unit circle showing cos(0) = 1 and sin(0) = 0īecause tangent equals sine divided by cosine, tan(0) = sin(0) / cos(0) = 0 / 1 = 0. Since it makes sense to start at 0 degrees, our circle will look like this: Fig 4. Important angles and their corresponding sine, cosine and tangent values A complete circle – 360 degrees.ĪDVERTISEMENT Part 2. The measure increases in a counterclockwise direction, so the point with coordinates (0, 1) will correspond with 90 degrees.
The point with coordinates (1, 0) corresponds with 0 degrees (see Fig 1). The angles can be measured in degrees and/or radians. Thus, by moving around the circle and changing the angle, we can measure sine and cosine of that angle by measuring the y and x coordinates accordingly. Similarly, the x coordinate will equal cos(α), or x = cos(α).
x coordinate = cos(α) and y coordinate = sin(α)Īs a result, the y coordinate of the point where the triangle touches the circle equals sin(α), or y = sin(α). Next, let's move this triangle into our Unit Circle, so the radius of the circle can serve as the hypotenuse. Similarly, cosine will equal the length of AC. Since the hypotenuse equals 1 and anything divided by 1 equals itself, sin of alpha equals the length of BC. Geometric definition of sine and cosine for an angle with hypotenuse equal 1 The triangle below reminds us how we define sine and cosine for some angle alpha. Having a radius equal 1 unit will allow us to create reference triangles with hypotenuse equal to 1 unit.Īs we will see shortly, that allows us to measure sine, cosine and tangent directly. The graph of the unit circle with radius = 1 and points of intersection with X and Y axes In other words, the center is put on a graph where the X and Y axes cross. The unit circle is a circle with a radius of one unit with its center placed at the origin. What is the Unit Circle and how is it used? Let's learn more about it and test our understanding with a handy trigonometric calculator I created at the end of the article. It removes the need for memorizing different values and allows the user to simply derive different results for different cases. The key to its usefulness is its simplicity. The unit circle is a useful visualization tool for learning about trigonometric functions.


 0 kommentar(er)
0 kommentar(er)
